本文共 6360 字,大约阅读时间需要 21 分钟。
文章目录
1:上传文件到阿里云的两种方法
我们以后的上传文件,是通过后台界面,点击上传,把图片保存到阿里与的bucket里的,并且拿到这个图片的真正地址,那我们要怎么做呢?
第一种:用户通过浏览器,选择文件上传,把图片先上传给应用服务器(把整个文件上传请求提交给网关,然后在交给商品服务,商品服务拿到图片流了,在使用java代码把图片的流数据,传给对象储存,最终存在bucket里面,并拿到地址)
缺点:我们文件上传还要过到我们的应用服务器里面(完全没必要,服务器会在大量的流量下,带来瓶颈) 优点:我们要上传到阿里云的bucket与我们的账号密码有关,但是这个东西不可以暴露,使用第一种方式的安全自处在于,文件交给我们的服务器,服务器用账号密码上传给阿里云 第二种:用浏览器直接上传给对象,我们将阿里云的账号密码直接写在js代码里面,让js控制,把表单直接提交给阿里云,风险就是泄露了阿里云的账号密码,所以我们可以使用服务端签名后直传,我们把操作对象的需要的账号密码直接存储在应用服务器里面,浏览器想要给阿里云上传数据,怎么办呢?上传之前先找我们的应用服务器,要到一个policy,服务器利用阿里云的账号密码,生成一个防伪签名(包含访问阿里云的授权令牌,以及我们要上传文件的地址),我们前端拿到这些信息以后,在带着这些信息(没有账号密码,只有防伪签名),以及要上传的文件,交给OSS,OSS验证这些是正确的就成功保存
第二种:用浏览器直接上传给对象,我们将阿里云的账号密码直接写在js代码里面,让js控制,把表单直接提交给阿里云,风险就是泄露了阿里云的账号密码,所以我们可以使用服务端签名后直传,我们把操作对象的需要的账号密码直接存储在应用服务器里面,浏览器想要给阿里云上传数据,怎么办呢?上传之前先找我们的应用服务器,要到一个policy,服务器利用阿里云的账号密码,生成一个防伪签名(包含访问阿里云的授权令牌,以及我们要上传文件的地址),我们前端拿到这些信息以后,在带着这些信息(没有账号密码,只有防伪签名),以及要上传的文件,交给OSS,OSS验证这些是正确的就成功保存 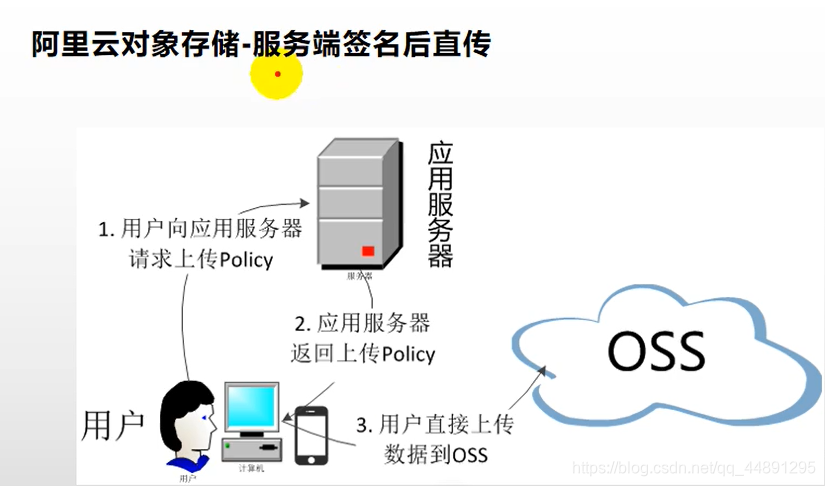
2:OSS的整合测试
我们进行阿里云对象存储——普通上传方式的演示
接下来,我们用阿里云文档里面的代码来做部分演示
第一步:在Maven项目中加入依赖项(推荐方式)
在Maven工程中使用OSS Java SDK,只需在pom.xml中加入相应依赖即可com.aliyun.oss aliyun-sdk-oss 3.10.2
第二步:添加权限,编写代码(endpoint ,accessKeyId ,accessKeySecret 都是要用到自己的bucket中,和自己创建密钥)
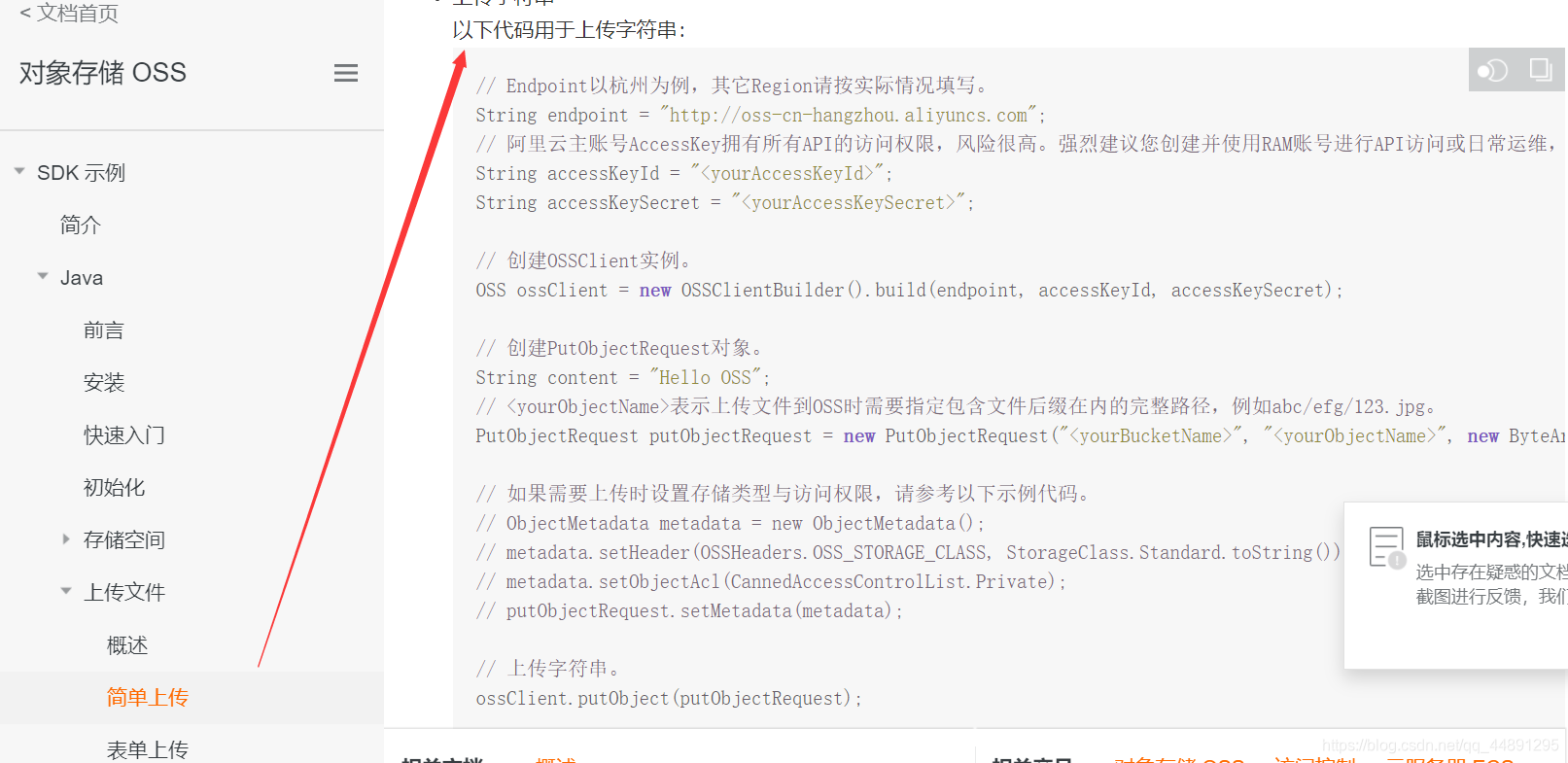
// Endpoint以杭州为例,其它Region请按实际情况填写。 String endpoint = "http://oss-cn-hangzhou.aliyuncs.com";// 阿里云主账号AccessKey拥有所有API的访问权限,风险很高。强烈建议您创建并使用RAM账号进行API访问或日常运维,请登录 https://ram.console.aliyun.com 创建RAM账号。 // //LTAI4G4JYhHC8zKDrTqnPcWx // //fUi3rvtsE58srN8Hk6ZzawRO5Wg3pK String accessKeyId = "secretid"; String accessKeySecret = "secret";// 创建OSSClient实例。 OSS ossClient = new OSSClientBuilder().build(endpoint, accessKeyId, accessKeySecret);// 创建PutObjectRequest对象。 String content = "Hello OSS";//表示上传文件到OSS时需要指定包含文件后缀在内的完整路径,例如abc/efg/123.jpg。 PutObjectRequest putObjectRequest = new PutObjectRequest(" ", " ", new ByteArrayInputStream(content.getBytes()));// 如果需要上传时设置存储类型与访问权限,请参考以下示例代码。// ObjectMetadata metadata = new ObjectMetadata();// metadata.setHeader(OSSHeaders.OSS_STORAGE_CLASS, StorageClass.Standard.toString());// metadata.setObjectAcl(CannedAccessControlList.Private);// putObjectRequest.setMetadata(metadata);// 上传字符串。 ossClient.putObject(putObjectRequest);// 关闭OSSClient。 ossClient.shutdown();
 更简单的方式是我们使用 SpringCloud Alibaba-OSS对象存储(它已经封装好了),如下进行演示 第一步:配置依赖
更简单的方式是我们使用 SpringCloud Alibaba-OSS对象存储(它已经封装好了),如下进行演示 第一步:配置依赖 com.alibaba.cloud aliyun-oss-spring-boot-starter
第二步:配置accessKeyId, secretAccessKey and region in application.properties.
// application.propertiesalibaba.cloud.access-key=your-akalibaba.cloud.secret-key=your-skalibaba.cloud.oss.endpoint=***
第三步:写测试类
@Autowired private OSSClient ossClient; @Test void saveFile() throws FileNotFoundException { // download file to local InputStream content = new FileInputStream("D:\\图片\\2.png"); ossClient.putObject("mall-zlj", "2.png"),content); } 完成即可在后端上传文件到阿里云,如果我们在搭配上前端界面,一个完整的普通上传方式就完成了
缺点:我们文件上传还要过到我们的应用服务器里面(完全没必要,服务器会在大量的流量下,带来瓶颈) 优点:我们要上传到阿里云的bucket与我们的账号密码有关,但是这个东西不可以暴露,使用第一种方式的安全自处在于,文件交给我们的服务器,服务器用账号密码上传给阿里云3:OSS获取服务端签名
我们进行阿里云对象存储——服务端签名后直传
阿里官方参考文档
大家认真看上面的文档,你就可以知道为什么要用服务端签名后直传和他是什么怎么用我们自己写一个mall-third-party微服务来管理我们的第三方服务
第一步:导入mall-common依赖(里面有nacos 服务中心,配置中心)和aliyun-sdk-oss,记得加上@EnableDiscoveryClient注解和配置nacos注册中心
server: port: 60000spring: cloud: nacos: discovery: server-addr: localhost:8848 application: name: mall-third-party
com.atstudying.mall mall-common 0.0.1-SNAPSHOT com.baomidou mybatis-plus-boot-starter com.aliyun.oss aliyun-sdk-oss 3.10.2
第二步::我们去阿里云对象存储 OSS帮助文档中,找到应用服务器核心代码解析一块的内容导入,并做一定的修改
@RestControllerpublic class OSSController { @Value("${spring.cloud.alicloud.access-key}") private String accessId; @Value("${spring.cloud.alicloud.secret-key}") private String accessKey; @Value("${spring.cloud.alicloud.oss.endpoint}") private String endpoint; @Value("${spring.cloud.alicloud.oss.bucket}") private String bucket; @RequestMapping("/oss/policy") public Map policy(HttpServletRequest request, HttpServletResponse response)throws ServletException, IOException { ////https://mall-zlj.oss-cn-beijing.aliyuncs.com/1.png String host = "https://" + bucket + "." + endpoint; // host的格式为 bucketname.endpoint //希望生成一个日期目录,这样,方便我们去看,所以我们使用日期格式化的结果 String format = new SimpleDateFormat("yyyy-MM-dd").format(new Date()); String dir = format+"/"; // 用户上传文件时指定的前缀。 //其实这一个代码,我们可以不使用了,我们可以直接注入OssClient // 创建OSSClient实例。 OSS ossClient = new OSSClientBuilder().build(endpoint, accessId, accessKey); try { long expireTime = 30; long expireEndTime = System.currentTimeMillis() + expireTime * 1000; Date expiration = new Date(expireEndTime); // PostObject请求最大可支持的文件大小为5 GB,即CONTENT_LENGTH_RANGE为5*1024*1024*1024。 PolicyConditions policyConds = new PolicyConditions(); policyConds.addConditionItem(PolicyConditions.COND_CONTENT_LENGTH_RANGE, 0, 1048576000); policyConds.addConditionItem(MatchMode.StartWith, PolicyConditions.COND_KEY, dir); String postPolicy = ossClient.generatePostPolicy(expiration, policyConds); byte[] binaryData = postPolicy.getBytes("utf-8"); String encodedPolicy = BinaryUtil.toBase64String(binaryData); String postSignature = ossClient.calculatePostSignature(postPolicy); Map respMap = new LinkedHashMap (); respMap.put("accessid", accessId); respMap.put("policy", encodedPolicy); respMap.put("signature", postSignature); respMap.put("dir", dir); respMap.put("host", host); respMap.put("expire", String.valueOf(expireEndTime / 1000)); return respMap; //上面的数据最终以跨域的形式返回出去,下面的跨域,我们最终在网关统一解决,我们就可以注释掉下面的代码 } catch (Exception e) { // Assert.fail(e.getMessage()); System.out.println(e.getMessage()); } finally { ossClient.shutdown(); } return null; }} 第三步:启动mall-third-party,进行如下访问
http://localhost:60000/oss/policy 我们要把前端所有请求转交给网关,网关在转交给mall-third-party 所以配置网关配置:
我们要把前端所有请求转交给网关,网关在转交给mall-third-party 所以配置网关配置:  http://localhost:88/api/thirdparty/oss/policy访问即可
http://localhost:88/api/thirdparty/oss/policy访问即可 完成即可在前端上传文件到阿里云,如果我们在搭配上前端界面,一个完整的服务端签名后直传的方式就完成了
优点:我们文件上传就不会过到我们的应用服务器里面(服务器会在大量的流量下,带来少的瓶颈)转载地址:http://wzhq.baihongyu.com/